第４回　「ねじれの位置の見つけ方」　（中学１年生・数学）

皆さんこんにちは！

問題解説シリーズ第４回目です。

今回は中１数学の図形分野です。おそらく多くの学校で次回の定期テスト（学年末テスト）の範囲となるところです。

その中でも苦手としている子が多い「ねじれ」の見つけ方について解説していきます。

「平行」や「垂直」（交わっている辺）は見つけられるけど、「ねじれ」はどうもうまくいかない…という子が非常に多いです。

アップステーション流の解き方でマスターしていきましょう。

 

【例題】

よく見かけるねじれの問題ですね。

それでは、まず一般的な解法を見ていきましょう。

 

一般的な解法…

ねじれの位置 ･･･ 空間上に，平行でなく，交わらない2つの直線の位置のこと

したがって、答えは辺DC・HG・AD・EH

 

この説明だけでねじれの位置を見抜くことが出来れば問題ありません。しかし実際に教えていると全てきちんと答えられない子が多いです。

今回の問題は「４つの辺を全て答える」ことがポイントなのですが、２つ・３つに留まってしまう場合が多いです。

ではきちんと全部見抜くためには，どのようにしたらいいでしょうか。

 

アップステーション流の解法…

ねじれの位置…「平行でもなく」「交わってもいない」辺のこと。

したがって、この２つを消して残ったもの＝ねじれです。

実際にやってみましょう！

 

 

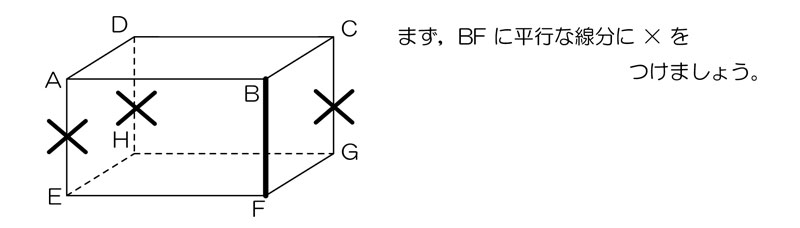
↑まず「平行」に×印をつけていき…

 

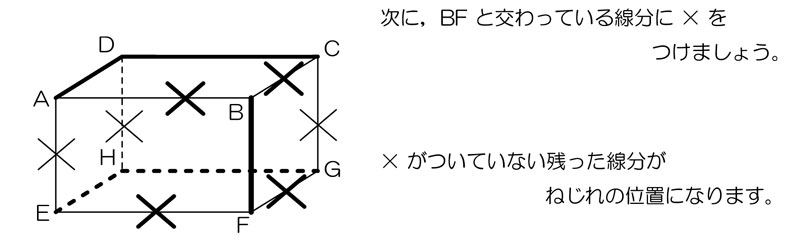
↑「交わっている」ものにも×をつけます。

 

のこりもの＝ねじれということですね！つまり答えは辺DC・HG・AD・EHの４つです！

 

 

数学が得意な子にとってはすんなりと見つけられる当たり前のことかもしれませんが、特に図形が苦手な子にとっては難しい問題です。

その場合は、このように正解にたどり着くまでの手順を明確に示してあげることが大切です。

 

次回のテストで是非お試しあれ！